Junge Landschaft
Voluminös: Mathe im GaLaBau - Teil 1
von: Uwe Bienert127. Folge: Unsere Serie für den Nachwuchs erläutert das wichtigste GaLaBau-Grundlagenwissen vom Abstecken bis zum Zaunbau: Diesmal geht es um das Thema "Mathematik im Berufsalltag".
Ach ja, in den Ferien von Mathematik zu schreiben erscheint ein wenig wahnwitzig - um es einmal vorsichtig auszudrücken. Stimmt, aber… ich würde es nicht tun (auch für mich sind Ferien und Urlaub zwei heilige Sachen), wenn es nicht wichtig wäre.
Es gibt immer mehr Probleme in puncto Grundkenntnisse in den Hauptfächern (vor allem Mathematik) bei der Suche nach einem Ausbildungsplatz. Der alte Spruch meines Großvaters - "Hast du einen dummen Sohn, so schicke ihn zur Bauunion. Ist dein Sohn noch dümmer, als Gärtner geht es immer!" - ist inzwischen so realitätsfern wie "Blaue Elefanten".
Die Bauberufe und die Berufe des Baunebengewerbes sind in unserer modernen Zeit zu hoch technologisierten Berufen geworden. Dabei sollte man nicht nur an ein hohes technisches Niveau denken, sondern auch an eine sehr hohe Qualifikation des Führungspersonals und deren "Zuarbeiter" (Vorarbeiter, Poliere, Meister Techniker und dergleichen). Und genau hier setzen wir an:
NL-Stellenmarkt

Wozu braucht man im Leben Mathe?
Nun zugegeben, beim Denken an Differenzialgleichungen und Funktionen fällt einem nicht gleich der Gärtner als für die Nutzung dieses Wissens bevorzugte Berufsgruppe ein. Dennoch spielt Mathematik in unserem Beruf eine wichtige Rolle.
Landschaftsgärtner müssen präzise arbeiten. Räumliches Vorstellungsvermögen und ein Hang zu Mathematik erleichtern Landschaftsgärtnern ihre Arbeit erheblich.
Da stellt man sich unweigerlich die Frage: Wo fängt Mathe an und wo hört sie auf? Sie fängt bei Zahlen an. Zählen ist (auch wenn es hier albern klingt) eine wichtige Voraussetzung für mathematisches Verständnis. Da kann es bei dem einen oder anderen Zeitgenossen schon Schwierigkeiten geben.
Ein wichtiger Bestandteil der Mathematik ist das Messen. Irgendwo müssen die Zahlen ja herkommen die man "verarbeitet". Die Gewichtung von "Messen" ist im GaLaBau sehr hoch zu bewerten. Eigentlich vergeht kein Tag, an dem nicht irgendetwas gemessen oder auch gewogen wird. Hier werden auch die meisten Fehler gemacht, die nach der Verarbeitung der Ergebnisse verheerende Auswirkungen haben können.
Aus diesen Zahlen und Messungen ergibt sich der nächste Schritt - das Rechnen. Hierbei sollten vor allem die Grundrechenarten (vielen Bewerbern für den Beruf fällt es schon schwer diese zu nennen) Addition, Subtraktion, Multiplikation und Division ohne Wertverlust beherrscht werden. Im Weiten spielen Prozent-, Flächen-, Volumen-, Masse- und Zeitberechnungen eine wichtige Rolle bei der Baustellenabwicklung. Aber auch Analysen, Wahrscheinlichkeitsrechnung, lineare Funktionen, grafische Darstellung, Modelle und dergleichen spielen gerade in Führungspositionen eine große Rolle.
Mathematik zieht sich durch unseren gesamten Beruf und endet bei jedem Einzelnen auf der Lohn- oder Gehaltsabrechnung mit einem Betrag auf seinem Konto! Ich schlage vor, wir fangen beim "Urschleim" an und reden über Zahlen. Aber nur kurz, damit keiner gähnt!
Zahlen, Zahlen, Zahlen…
Der Begriff Zahl kommt aus dem Althochdeutschen (zala = eingekerbtes Merkmal) und wurde benutzt, um darzustellen, aus wie vielen Elementen eine Menge besteht.
In der Mathematik sind Zahlen abstrakte mathematische Objekte, also sie entstehen nur in unserem Kopf und werden erst im praktischen Bezug mit Leben erfüllt. Sicher einer der Gründe, warum ich in einigen Mathematik-Stunden nicht so ganz genau wusste, was der Mensch da vorn von mir wollte.
Das Konzept der natürlichen Zahlen, welche zum Zählen verwendet werden können und grundlegende Bedeutung besitzen, reicht bis in die Urgeschichte zurück. Und während vor über 4000 Jahren die Ägypter und Babylonier mit Brüchen (rationalen Zahlen) zu rechnen begannen und vor 2400 Jahren irrationale Zahlen nach griechischen Erkenntnissen eingeführt wurden, dachten die Inder im 7. Jahrhundert erstmals über die Null und negative Zahlen nach.
Die Idee imaginärer Zahlen, durch die die reellen Zahlen später zu den bedeutenden komplexen Zahlen erweitert wurden, reicht in die europäische Renaissance zurück. Aus diesem kurzen Abriss kann man schon den Schluss ziehen - Zahl ist nicht gleich Zahl.
Fakt ist: Für uns sind natürliche Zahlen die wichtigste Position in diesem Zahlenwirrwarr. Wer mehr wissen will (sicher eine überschaubare Anzahl), sollte sich im Netz umhören oder ein kluges Buch lesen.
Jetzt wird es praktisch…Die Messung
Eine Messung ist das Ausführen von geplanten Tätigkeiten zu einer quantitativen Aussage über eine Messgröße im Zusammenhang mit einer Einheit. Dabei ist die Messgröße jene physikalische Größe (Länge, Masse, Zeit, Temperatur und dergleichen), der die Messung gilt. Ziel einer Messung ist es, ein Messergebnis über eine unbekannte Größe eines Objekts als verlässliche Aussage zu erhalten.
Das Ergebnis der Messung ist im ersten Schritt ein Messwert, der aber eine Messabweichung (hier ist die recht nett umschriebene Ausrede für Messfehler versteckt) enthält und von seinem wahren Wert abweicht. Man unterscheidet zwischen direkter Messung und indirekter Messung. Bei der direkten Messung ist deren Ergebnis unmittelbar am Messmittel (Bandmaß, Uhr, Waage) ablesbar. Indirekte Messungen sind im GaLaBau nicht zu finden, es sei denn, jemand kommt auf die Idee, über das elektromagnetische Spektrum der Sonne deren Temperatur zu ermitteln. Kann man machen, aber muss man es auch?
Nochmal zurück zu den Fehlern. Oben lernen wir: Fehler (oder Abweichungen) sind unweigerlich anwesend! Viel wichtiger ist es zu erfragen: Wie sind die Fehler entstanden? Das kann unterschiedliche Ursachen haben:
- Das Messgerät lässt nur eine bestimmte Genauigkeit zu. Habe ich etwa eine Messlatte mit Zentimeter-Einteilung, ist es müßig, auf den Millimeter genau messen zu wollen. Ich muss die Millimeter schätzen - Fehlerursache!
- Es wurde ein unzweckmäßiges Messverfahren gewählt. Beispiel: Um die Entfernung von Berlin nach Leipzig zu ermitteln, ist sicher der Streckenzug genauer als die Möglichkeit, die Strecke abzuschreiten.
- Witterungsverhältnisse haben einen nicht zu unterschätzenden Einfluss auf bestimmte Messergebnisse. Man sollte es einmal selbst ausprobieren, die voll ausgeschobene Messlatte zur Ermittlung einer Baustellenhöhe bei Windstärke 6 oder 7 richtig senkrecht zu halten. Viel Spaß!
- Wenn während der Arbeit das Gerät versagt.
- … und dann der Mensch!!!
Fehlerquelle Mensch
Hierzu doch noch ein paar kurze Bemerkungen. Fehler sind dazu da, um aus ihnen zu lernen. Fehler sind also nicht so schlimm, nur ihre Wiederholung. Beim Messen sollte man immer den Kopf einschalten und über Zweckmäßigkeit seines Tuns nachdenken und die Konsequenzen abwägen. Dafür gibt es ein wichtiges Mittel - die Selbstkontrolle.
Lieber einmal mehr kontrolliert und damit den Messfehler minimiert, als völlig danebengelegen.
Die Methode bringt's
Es gibt motivierte, unmotivierte und übermotivierte Mitarbeiter. Während der Motivierte die effektivsten Ergebnisse auf schnellsten Weg bringt und der Unmotivierte gar nicht erst zu solchen Messungen hinzugezogen wird, ist der Übermotivierte eine echte Gefahr für den Erfolg. Er zweifelt sein Ergebnis immer an und versucht durch nochmaliges Messen noch besser zu werden - um dann am Ende doch zu scheitern. Ihm fehlt das Einschätzungsvermögen für die Zweckmäßigkeit seines Tuns. Diesen Mitarbeitertyp gibt es überall - angefangen beim Azubi bis hin zum Firmenchef. Vielleicht ein Beispiel: In einer inzwischen nicht mehr existierenden Bildungsstätte für überbetriebliche Ausbildung im mitteldeutschen Raum stand die Höhenmessung mit Nivelliergerät (einfaches Baunivellier) auf dem Lehrplan. Dafür war von den Anleitern eine Strecke mit Kontrolldaten vorbereitet worden - zehn Messpunkte auf rund 300 m. Es gab einen Genauigkeitsschlüssel nfür die Notenfindung, in dem die Note 1 mit einer Genauigkeit von 0- mm festgelegt wurde. Um die Auswertung zu erleichtern, wurden Annfangs- und Endpunkt auf den gleichen Punkt festgelegt. Das Rennen war eröffnet! Um also die Note 1 zu erreichen, hätte man am Endpunkt mit einem Höhenunterschied von ±-1 mm aufschlagen müssen. Einen Tag lang versuchten alle Azubis des Kurses immer wieder das Ziel zu erreichen und alle waren begeistert.
Nicht nur, dass der ganzen Aktion der praktische Bezug verloren ging, weil im GaLaBau und auch sonst im Baugewerbe eine Abweichung von 1mm Höhenunterschied auf 300 m keine Rolle spielt. Es wurde auch der Selbstkontrollmechanismus der Teilnehmer zunehmend außer Kraft gesetzt, da die Genauigkeit der Zwischenpunkte in der Überprüfung keine Rolle spielten. Man hätte also ein Superergebnis erreichen können, obwohl man beispielsweise bei Punkt 4 einen ganzen Meter zu hoch und bei Punkt 5 einen ganzen Meter zu tief abgelesen oder errechnet hätte.
Ich bin kein Mensch, der den Standpunkt vertritt, dass der Millimeter kein Maß ist. Ich denke jedoch, dass die Relationen gewahrt bleiben sollten. Bei Streckenmessungen in unserem Gewerbe ist der Millimeter tatsächlich zu vernachlässigen, da schon viele Normative von Bauteilen Toleranzen über einen Millimeter aufweisen. Beim Bau von Holzbauwerken (Pergolen, Zäunen und dergleichen), beim Treppenbau und ähnlichen technischen Einrichtungen ist das anders.
Kommen wir zum Kerngeschäft, dem Rechnen
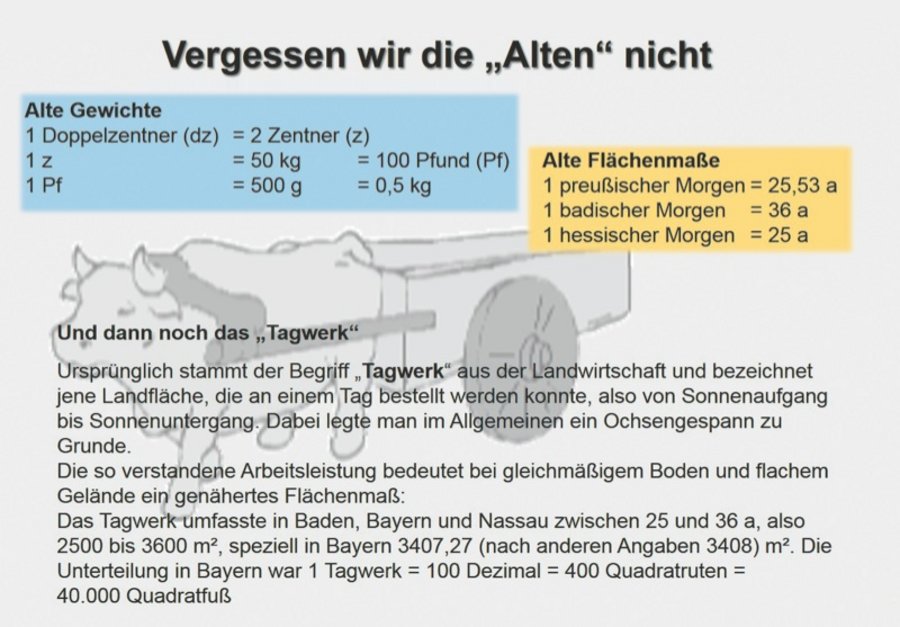
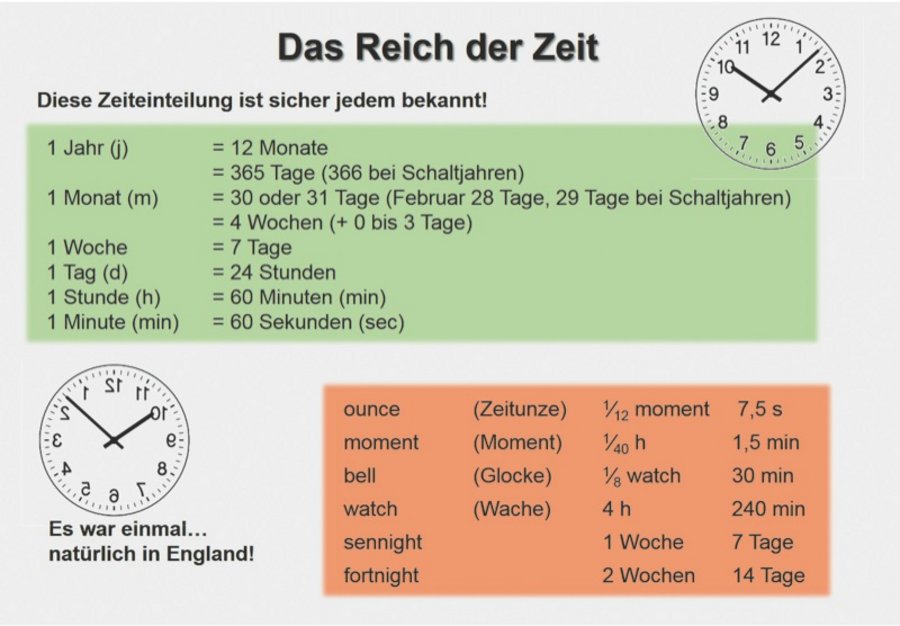
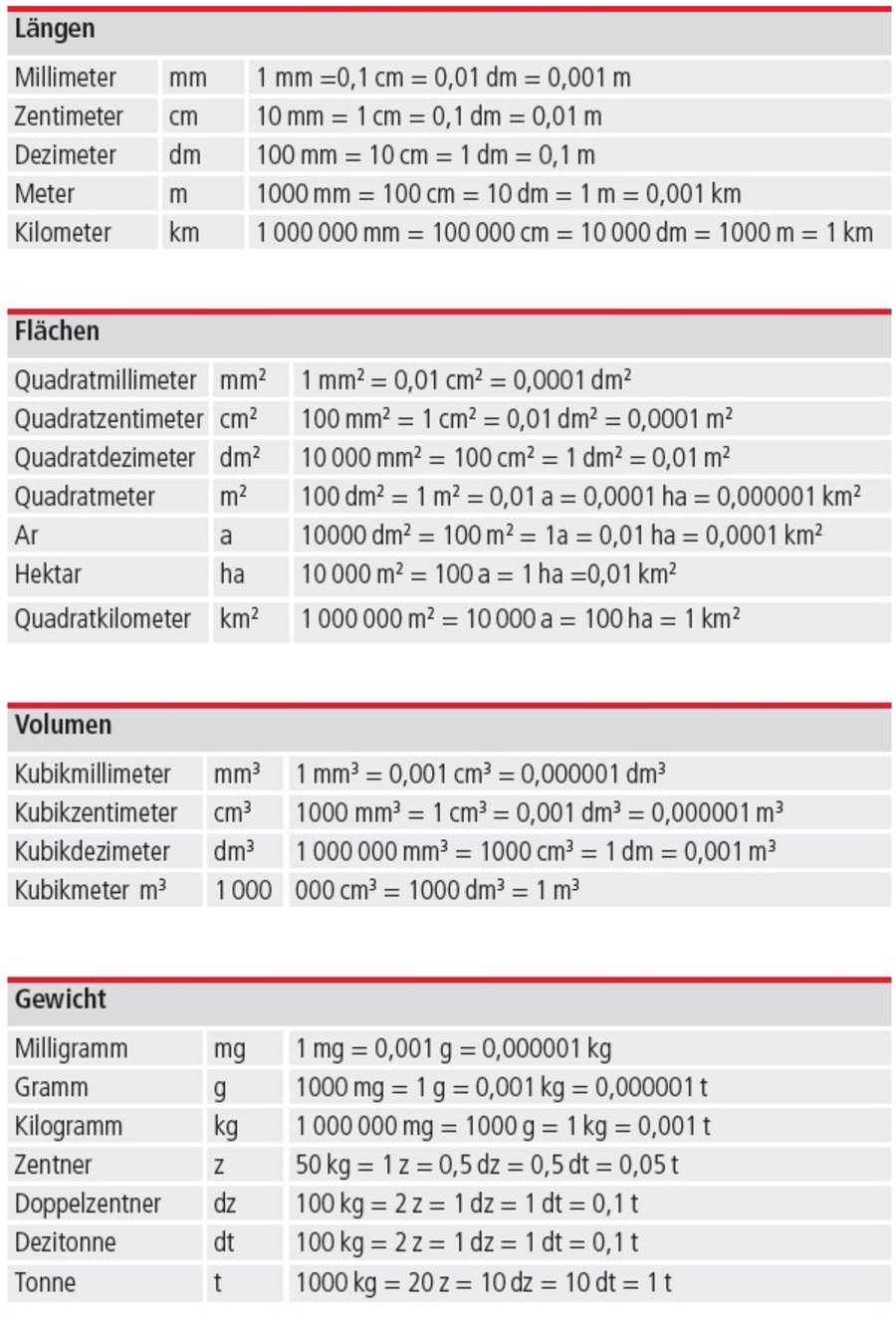
Dass wir für unsere mathematischen Unternehmungen nicht mehr in der Schule sitzen, merken wir nicht nur an unserer grünen Bekleidung, sondern vor allem daran, dass im Rechenprozess jetzt fast nichts mehr ohne eine Maßeinheit funktioniert. Also kein stumpfsinniges Zahlenjonglieren, sondern praxisbezogene Mathematik - Feldmathematik sozusagen. Dafür wurden in der Schule hoffentlich die Grundlagen gelegt, sonst wird es stressig. Wie war das nochmal mit den Maßeinheiten? Um langes Rätselraten zu vermeiden, folgt jetzt ein Überblick für die wichtigsten Maßeinheiten in unserem Beruf.
Im nächsten Heft soll es unter anderem um Grundlagen für die Berechnung von Flächen und Volumen gehen, um danach zu den praxisbezogenen Berechnungen für unseren Beruf (Wegebau, Teichbau, Aushub und dergleichen) zu kommen.
Uwe Bienert
Quellen:
Der Gärtner 15 (Klaus Herold; Ulmer-Verlag), Flächen und Volumen von Figuren und Körpern (Bernhard Ksiazek; Persen Verlag), Tafelwerke und Formelsammlungen (Cornelsen Verlag)
Nächsten Monat lesen Sie:
„Voluminös – Mathe im GaLaBau 2“.